(x y-10)dx (x-y-2)dy=0 191172-(x+y-10)dx+(x-y-2)dy=0

"main" 07/2/16 page 90 90 CHAPTER 1 FirstOrder Differential Equations 31 Consider the general firstorder linear differential equation dy dx p(x)y= q(x), (1925) wherep(x)andq(x)arecontinuousfunctionsonsome interval (a,b) (a) Rewrite Equation (1925) in differential form, and show that an integrating factor for the result

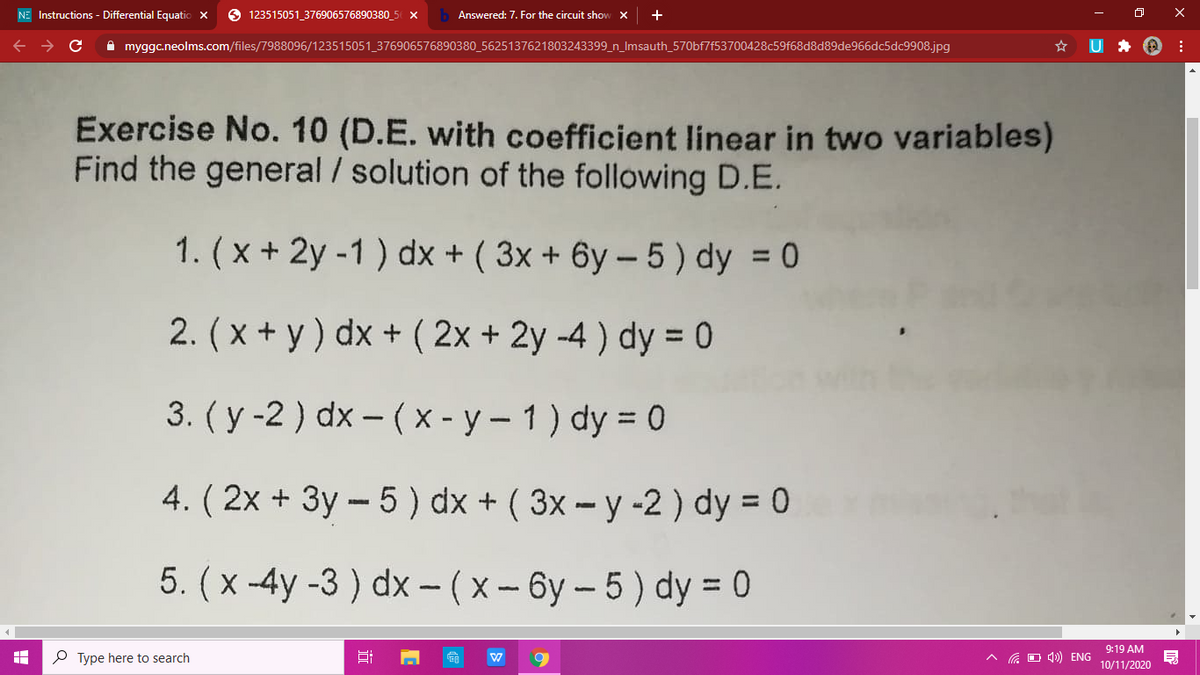
(x+y-10)dx+(x-y-2)dy=0-4 Answers4 Active Oldest Votes This answer is useful 2 This answer is not useful Show activity on this post If x 2 x y = 10, then y = 10 x − x (for x ≠ 0Δy Δx = f (x Δx) − f (x) Δx 4 Reduce Δx close to 0 We can't let Δx become 0 (because that would be dividing by 0), but we can make it head towards zero and call it "dx" Δx dx You can also think of "dx" as being infinitesimal, or infinitely small Likewise Δy becomes very small and we call it "dy", to give us dy dx = f (x dx

(x+y-10)dx+(x-y-2)dy=0のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y-10)dx+(x-y-2)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y-10)dx+(x-y-2)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y-10)dx+(x-y-2)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y-10)dx+(x-y-2)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y-10)dx+(x-y-2)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y-10)dx+(x-y-2)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y-10)dx+(x-y-2)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

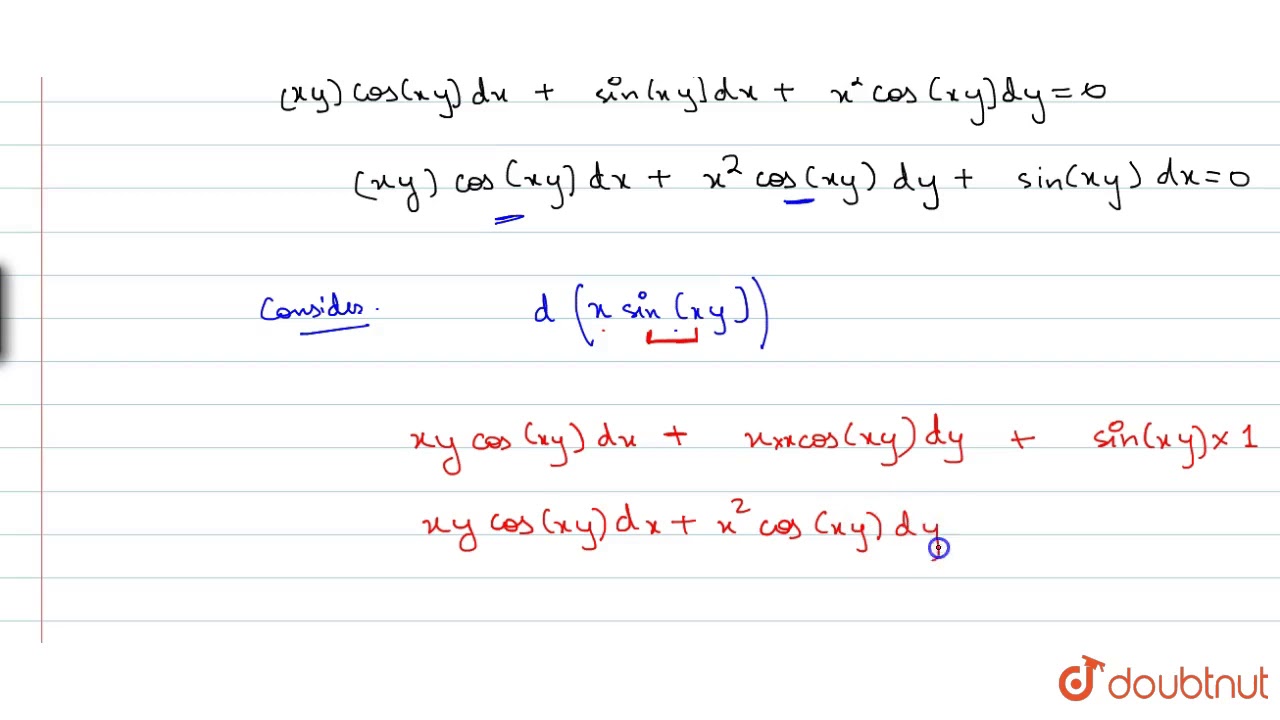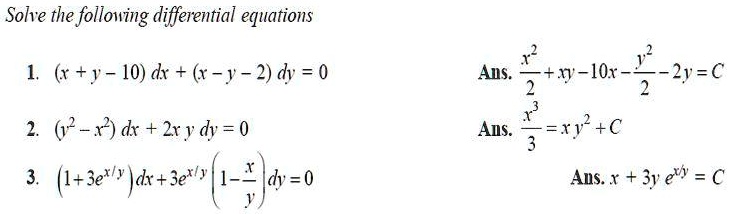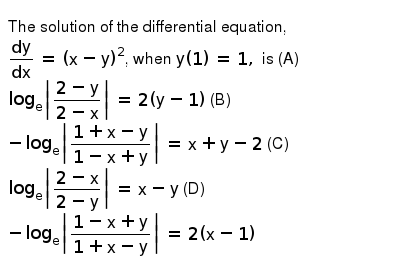「(x+y-10)dx+(x-y-2)dy=0」の画像ギャラリー、詳細は各画像をクリックしてください。

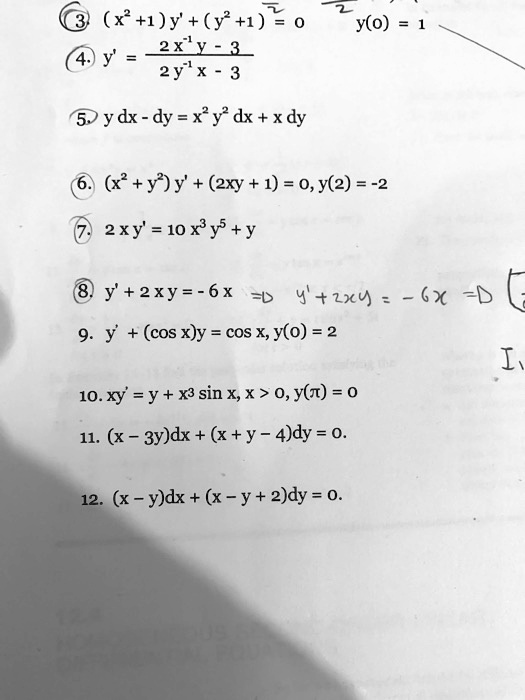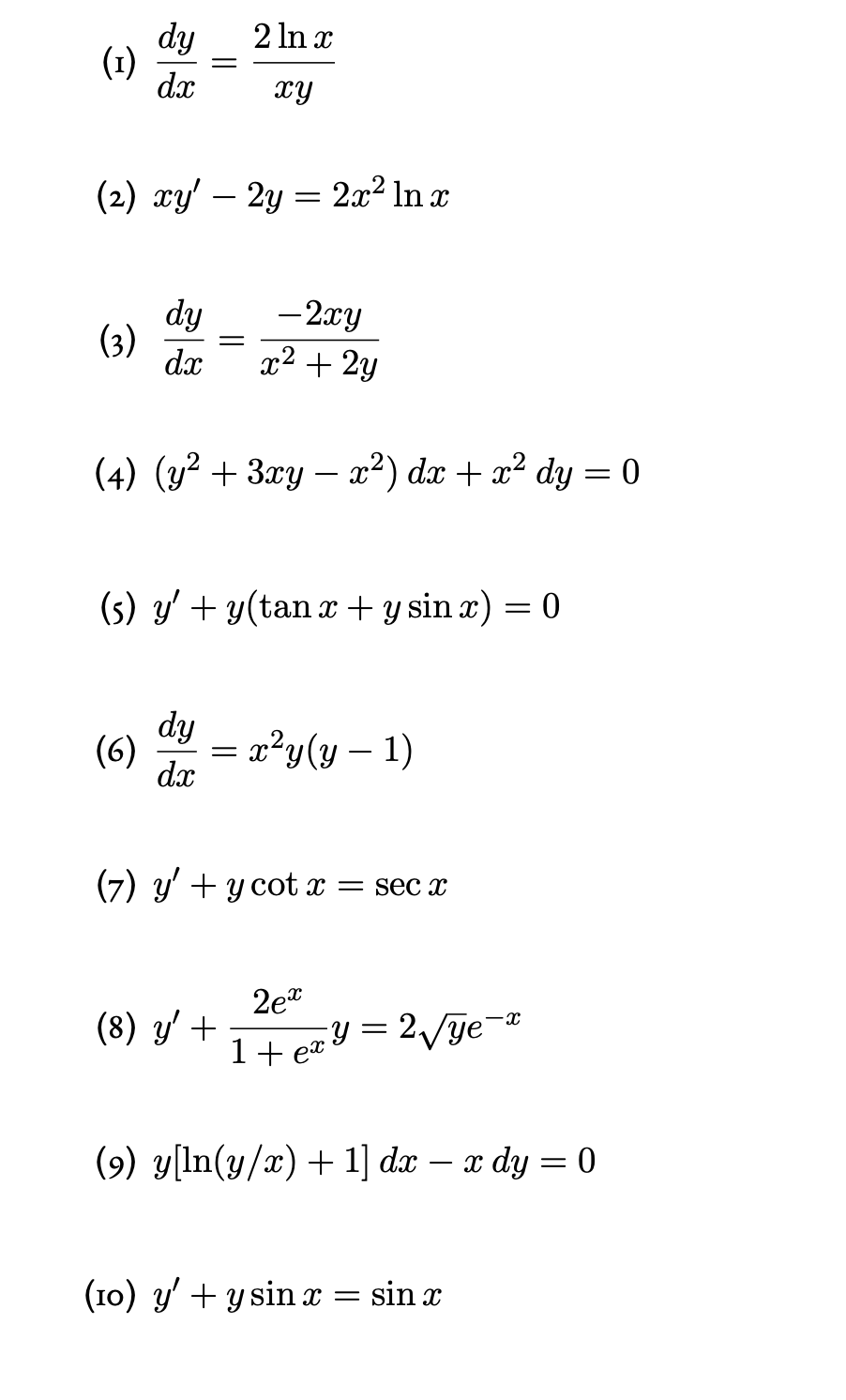 2xx(dy/dx)y=02x y 2xy x(dy/dx)=2xy /x /x dy/dx=(2xy)/(x) We're going to go back to the original equation and substitute 2 for every xterm (2)^22y=10 42y=104 4 2y=6 /2 /2 y=3 We're going to go back to dy/dx and substitute our values A solution of the differential equation (dy/dx)2 – x(dy/dx) y = 0 is (A) y = 2 (B) y = 2x2 – 4 y = 2x (D) y = 2x – 4 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries

Incoming Term: (x+y-10)dx+(x-y-2)dy=0,