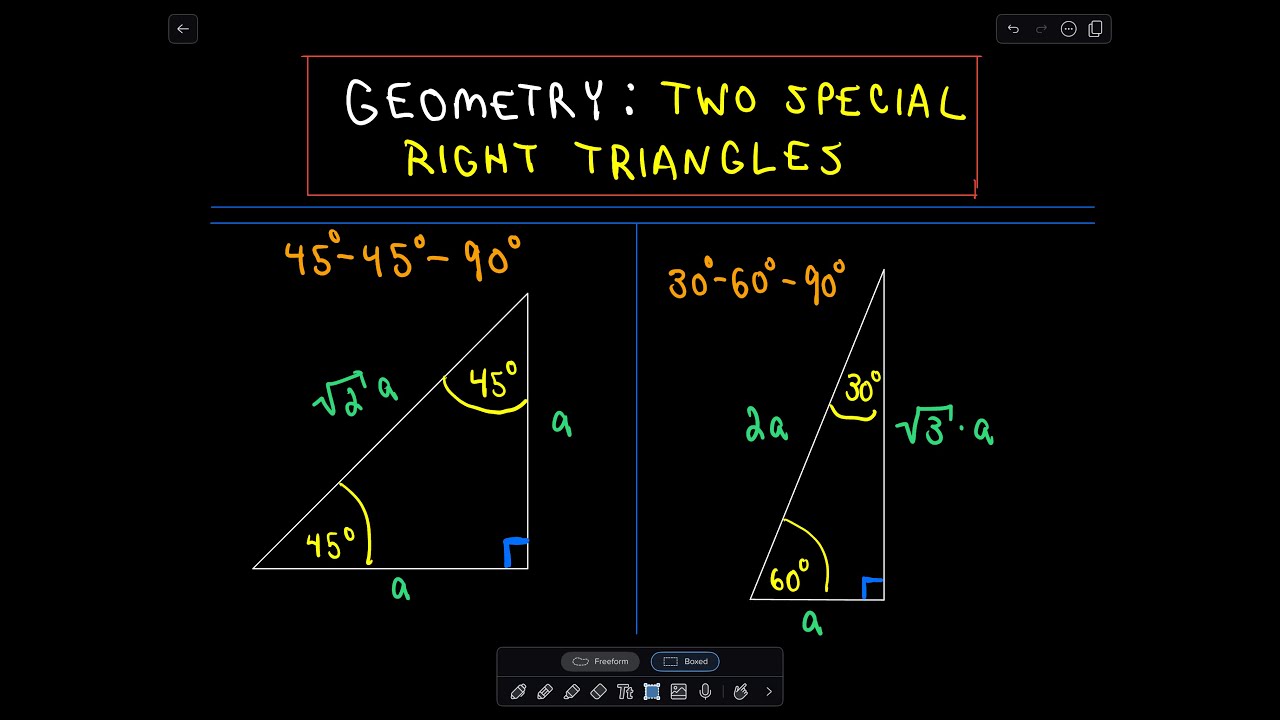
Triangles A triangle is a special right triangle defined by its angles It is a right triangle due to its 90° angle, and the other two angles must be 30° and 60° 345, and Right Triangles 345 and triangles are special right triangles defined by their side lengthsA triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides areThanks to all of you who support me on Patreon You da real mvps!
Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube
30 60 90 triangle side rules
30 60 90 triangle side rules-Watch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VIThe triangle is a special right triangle, as it has a special relationship between its sides If we know the measure of at least one side of the triangle, the special proportions of sides of the triangle could be used to determine the measure of other sides of the same triangle



45 45 90 And 30 60 90 Triangles Zona Land Education
The other one is the 45 45 90 triangle These triangles are special triangles because the ratio of their sides are known to us so we can make use of this information to help us in right triangle trigonometry problems In the case of the triangle, their side's ratios are 1The reason these triangles are considered special is because of the ratios of their sides they are always the same!Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles
Right triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculator 45 45 90 triangle calculator is a dedicated tool to solve this special right triangle Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator forMultiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuse
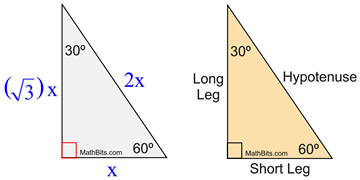
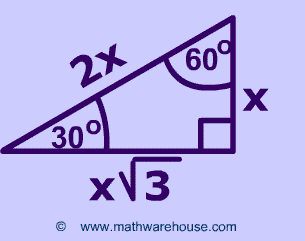
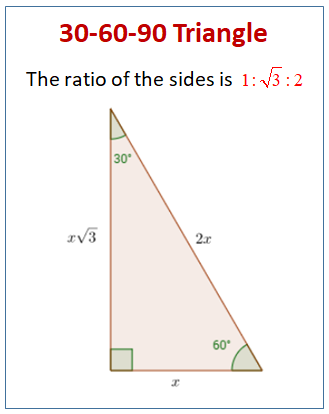
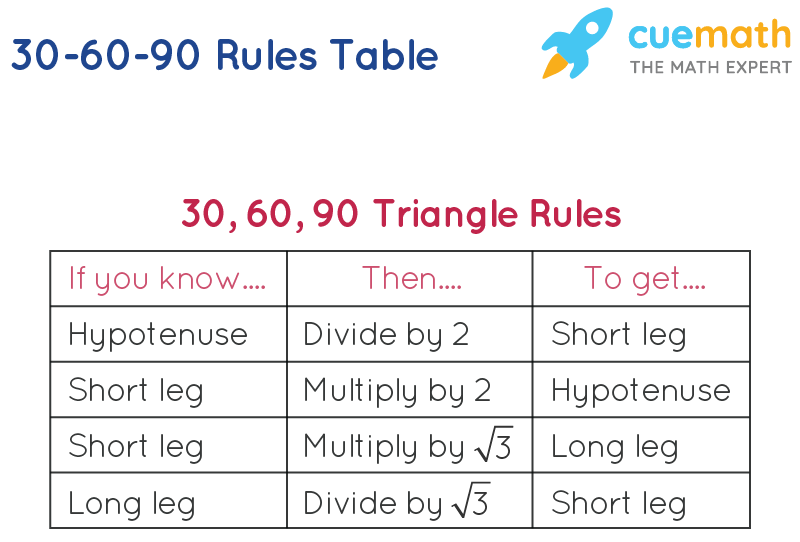
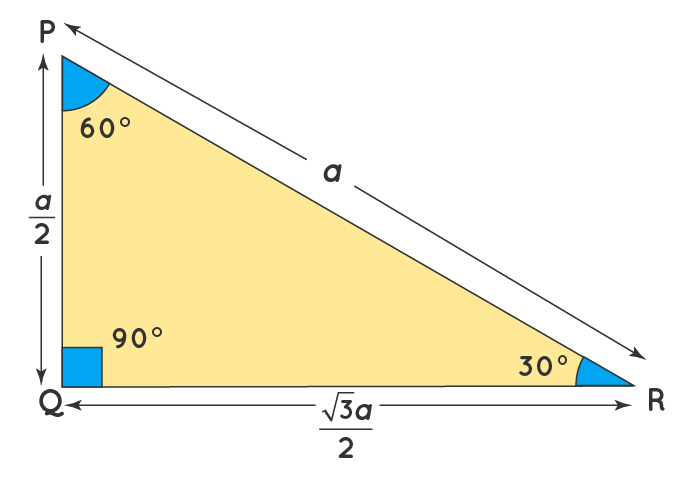
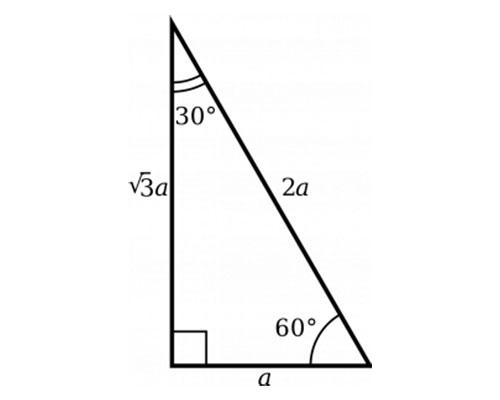
The property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5 Triangle Practice Name_____ ID 1 Date_____ Period____ ©v j2o0c1x5w UKVuVt_at iSGoMfttwPaHrGex rLpLeCkQ l ^AullN Zr\iSgqhotksV vrOeXsWesrWvKe`d\1Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60° 6) m n63The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




Special Right Triangles Review Article Khan Academy
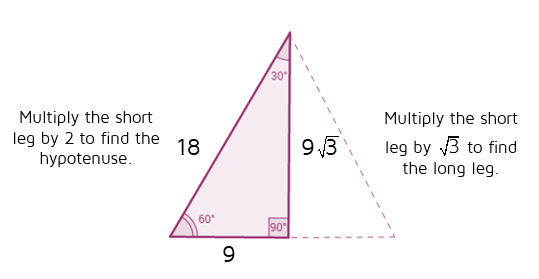
Another rule is that the two sides of the triangle or legs of the triangle that form the right angle are congruent in length Knowing these basic rules makes it easy to construct a triangle Constructing a Triangle The easiest way to construct a triangle is as follows Construct a square four equal sides to the Special right triangle 30 60 90 with hypothenuse measuring 8 cm The ratio for this special right triangle is {eq}1 \sqrt {3} 2 {/eq} We Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √ 3 Side opposite the 90° angle 2 x




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
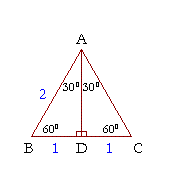
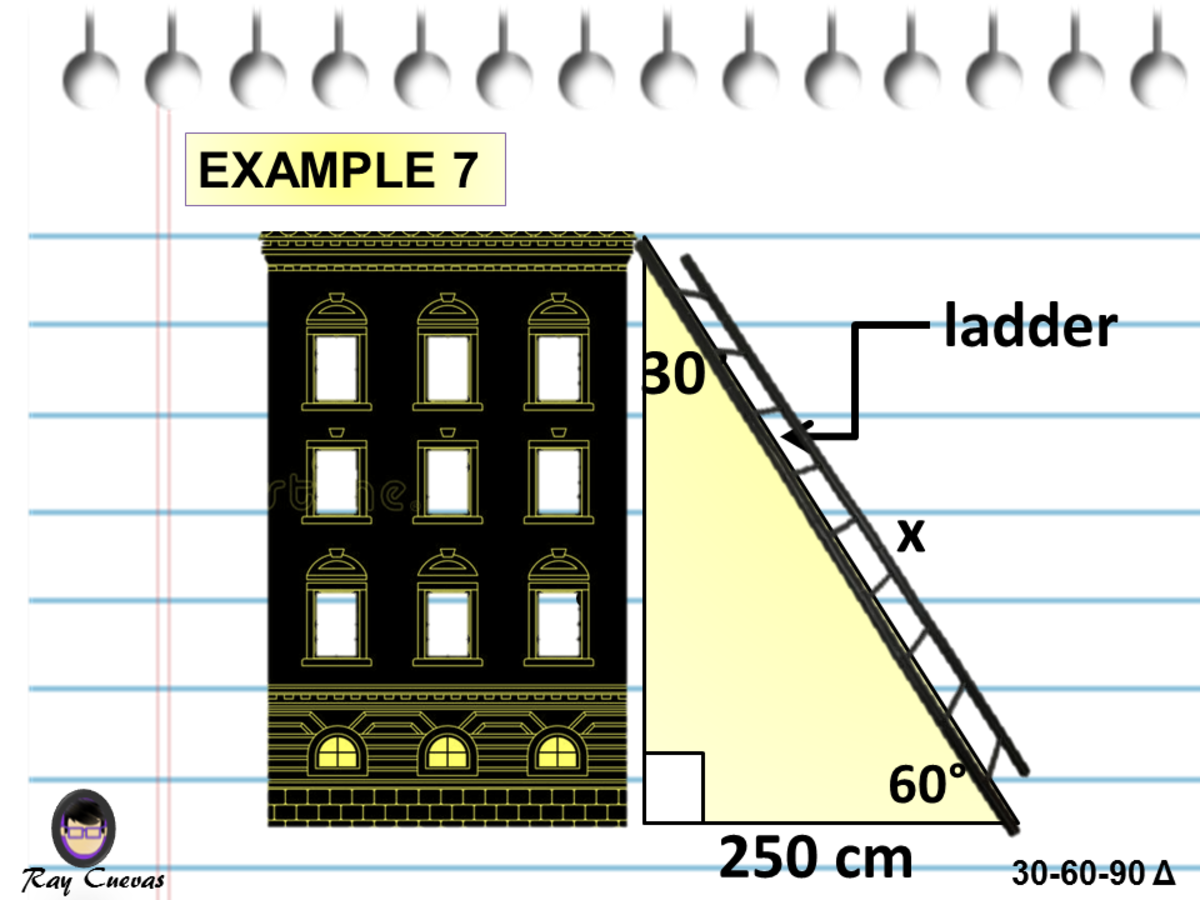
Draw a broad arc across PQ on the same side as point R Label the point where it crosses PQ as point A 8 With the compasses on A, draw a second arc, crossing the first arc at point B 9 Draw a line from Q, through B and on to cross the line PR Label the intersection point C 10 Done The triangle PQC is a triangleThe area of a triangle equals 1/2base * height Use the short leg as the base and the long leg as the height A thirty, sixty, ninety, triangle creates the following ratio between the angles and side length The side opposite the 30 degree angle equals x The side opposite the 60 degree angle is square root threeA theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class room




30 60 90 Triangle Definition Theorem Formula Examples




Special Right Triangles Fully Explained W 19 Examples
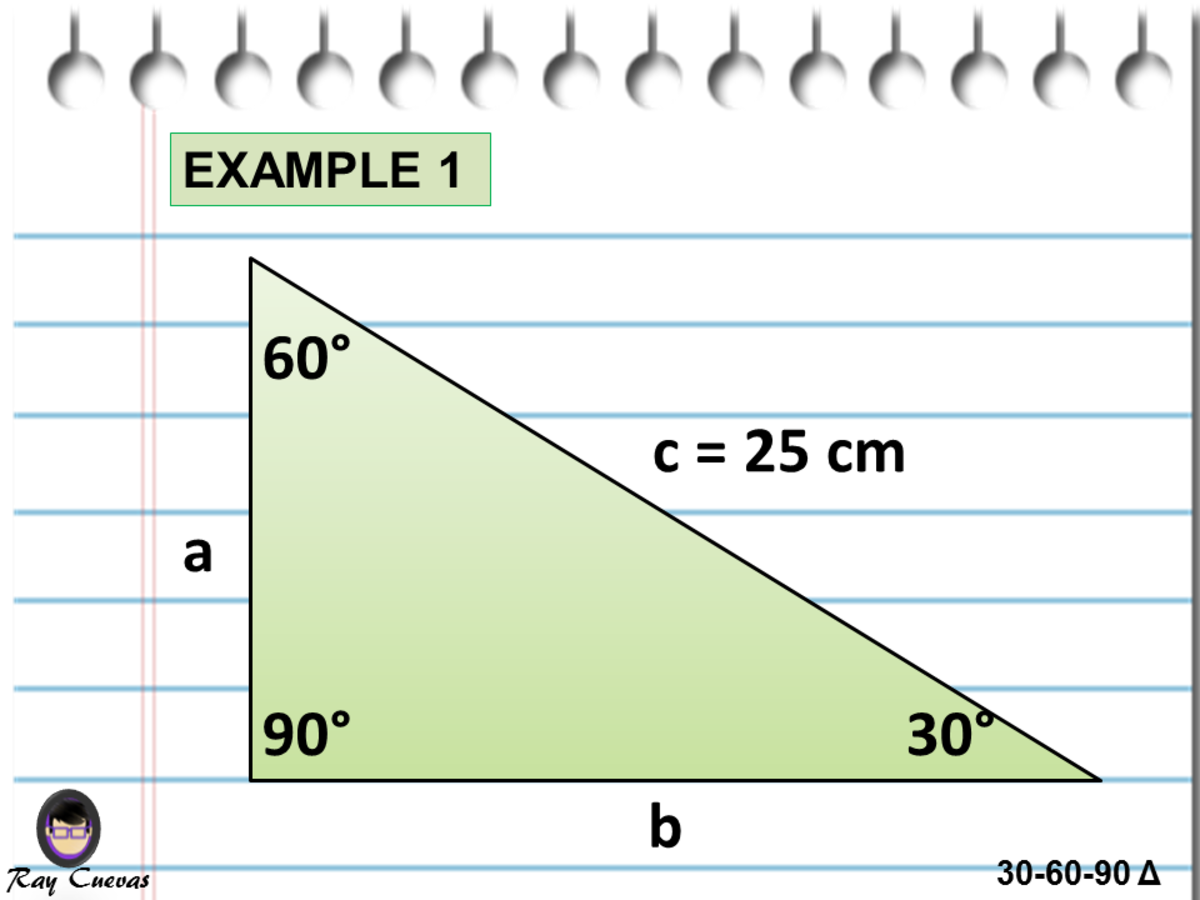
For any problem involving a 30°60°90° triangle, the student should not use a table The student should sketch the triangle and place the ratio numbers Since the cosine is the ratio of the adjacent side to the hypotenuse, you can see that cos 60° = ½ Example 2 Evaluate sin 30° Answer sin 30° = ½ You can see that directly in the figure above The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SATPlan Use the properties of a 30°60°90° Right Triangle to find the legs Add the sides to get perimeter Shorter Leg (SL) opposite the 30° angle = 1/2 Hypothenuse = 1/2 (8 cm) = 4 cm Longer Leg (LG) = √3 x shorter = 4√3 cm Perimeter (P) = Hypothenuse SL LG = 8 4 4√3 = 12 4√3 cm or P ≈ 13 cm



Lesson 1 Special Right Triangles 30 60 90 Frys Nc Math 2 Honors S2



Solve A 30 60 90 Triangle With Gradea
The third side of any triangle has a length that is BETWEEN the ____ and the ____ of the other two sides Difference and sum Example for third side rule of triangle known sides 6 & 123 rows As one angle is 90, so this triangle is always a right triangle As explained above that it isSee also Side /angle relationships of a triangle In the figure above, as you drag the vertices of the triangle to resize it, the angles remain fixed and the sides remain in this ratio Corollary If any triangle has its sides in the ratio 1 2 √3, then it is a triangle



Right Triangles Gmat Free



30 60 90 Triangles P4 Kate S Math Lessons
A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, andThe triangle is also a right triangle The Formulas of the Given that X is the shortest side measure, we know we can measure out at the baseline for length X , turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side at The triangle rule is for finding the the lengths of two sides when one side is given The shorter side is opposite the 30 degree angle, the longer side is opposite the 60 degree angle, and




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Calculator Formula Rules
A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangleThe triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to use Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is



What Are Some Differences And Similarities Between 30 60 90 Triangles And 45 45 90 Triangle Quora




30 60 90 Triangle Theorem Ratio Formula Video
The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2The sides of a triangle have a set pattern The side that is opposite to the 30° angle, 'y' will always be the smallest since 30° is the smallest angle in this triangle The side that is opposite to the 60° angle, y√3 will be the medium length because All degree triangles have sides with the same basic ratio Two of the most common right triangles are and degree triangles If you look at the 30–60–90degree triangle in radians, it translates to the following In any triangle, you see the following The shortest leg is across from the 30degree angle



3




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angle 45° For example, sin(45°), read as the sine of 45 degrees, is the ratio of the side opposite the$1 per month helps!!Special right triangles hold many applications in both geometry and trigonometry In this lesson you will learn the general formula for the ratios, and how to find missing sides of any 30 60 90 right triangle



30 60 90 Right Triangle Side Ratios Expii
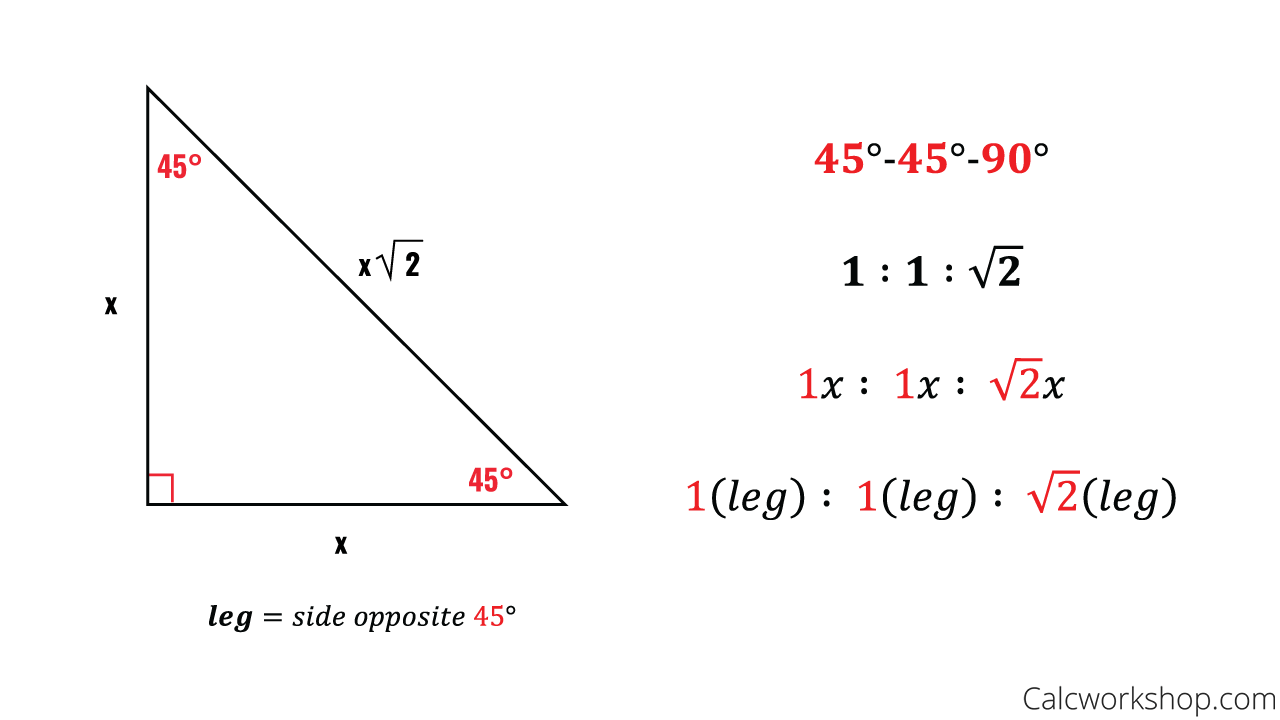



Special Right Triangles Fully Explained W 19 Examples
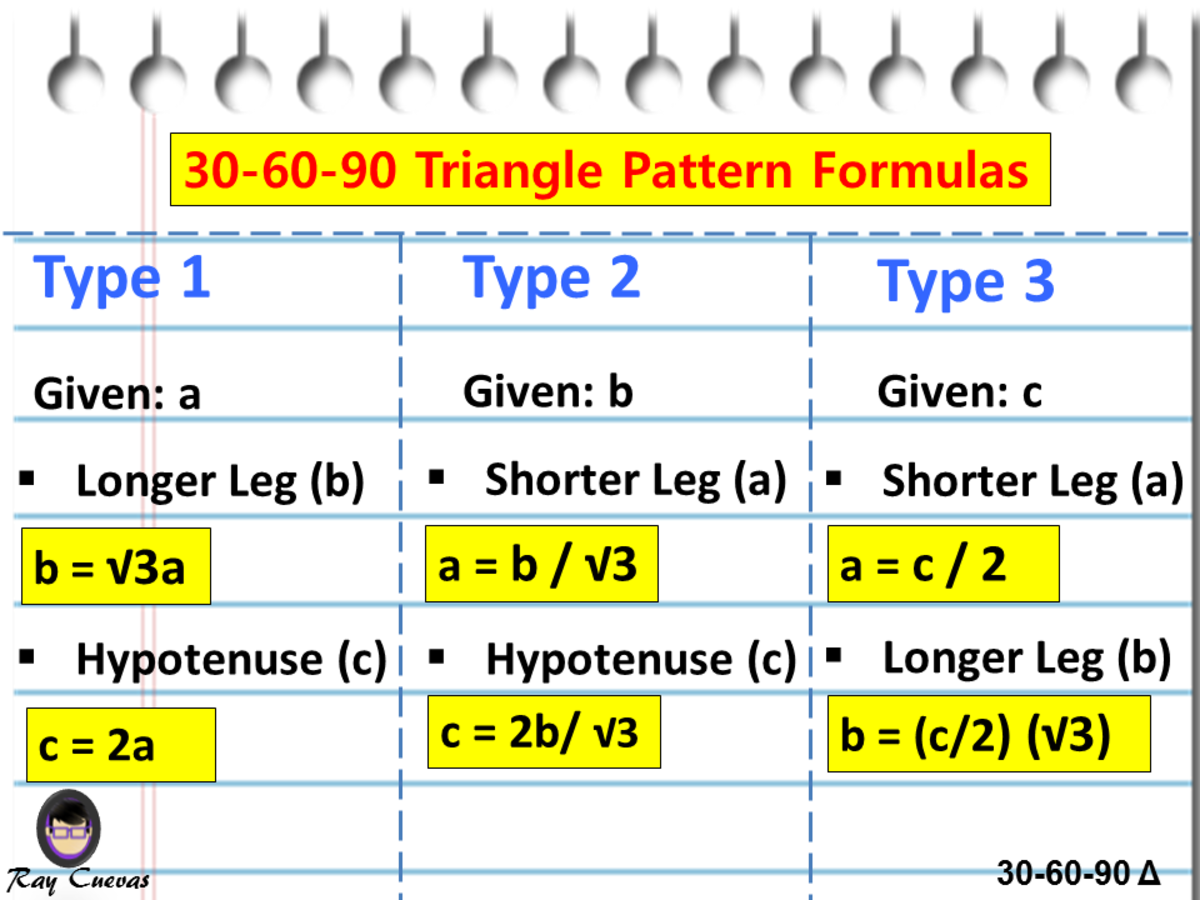
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!Special Right Triangles in A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another These relationships are




Special Right Triangles Review Article Khan Academy



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each otherLearn your way around two of the most common right triangles in mathematic equations triangles and degree triangles30 60 90 and 45 45 90 Triangle Calculator I N S T R U C T I O N S Start by entering the length of a triangle side Then click on which type of side it is The 5 choices you have are As soon as you click that box, the output boxes will automatically get filled in by the calculator Clicking "RESET" clears all of the boxes



30 60 90 Triangle Rules




Act Set 6 Special Right Triangle Rules Flashcards Quizlet



The Easy Guide To The 30 60 90 Triangle




Learn About The 30 60 90 Triangle Caddell Prep Online




30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




30 60 90 Triangle Calculator Formula Rules



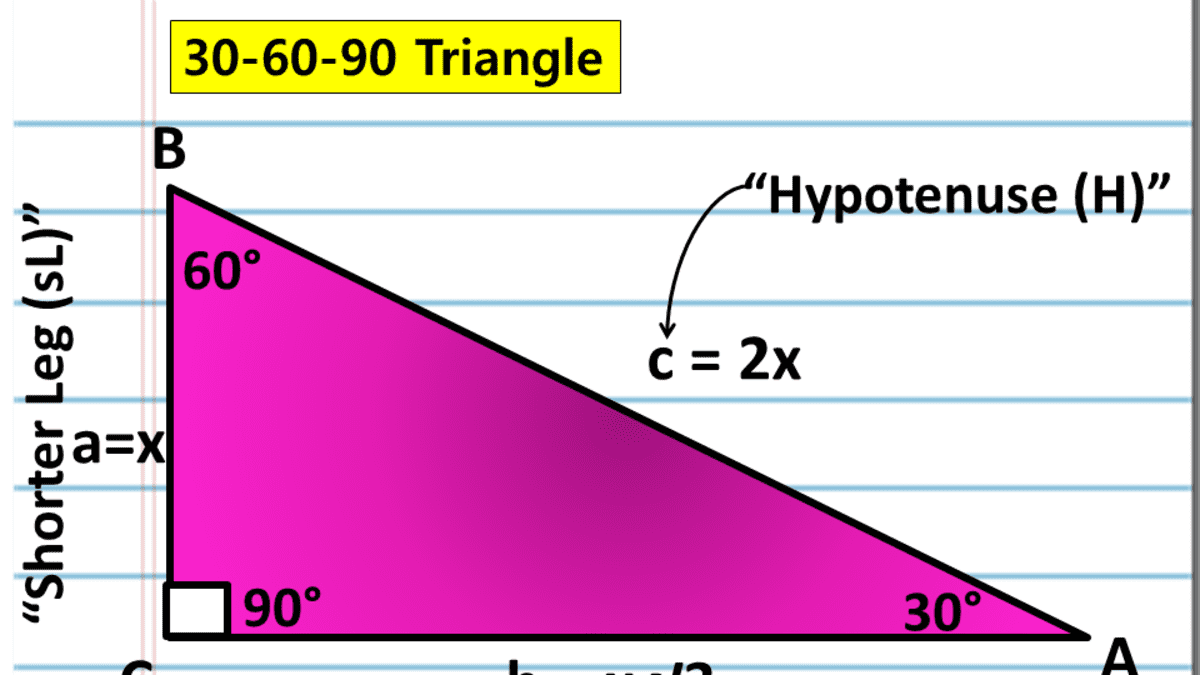
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Special Right Triangle Calculator Inch Calculator




30 60 90 Triangle Definition Theorem Formula Examples




45 45 90 Triangle Calculator Formula Rules



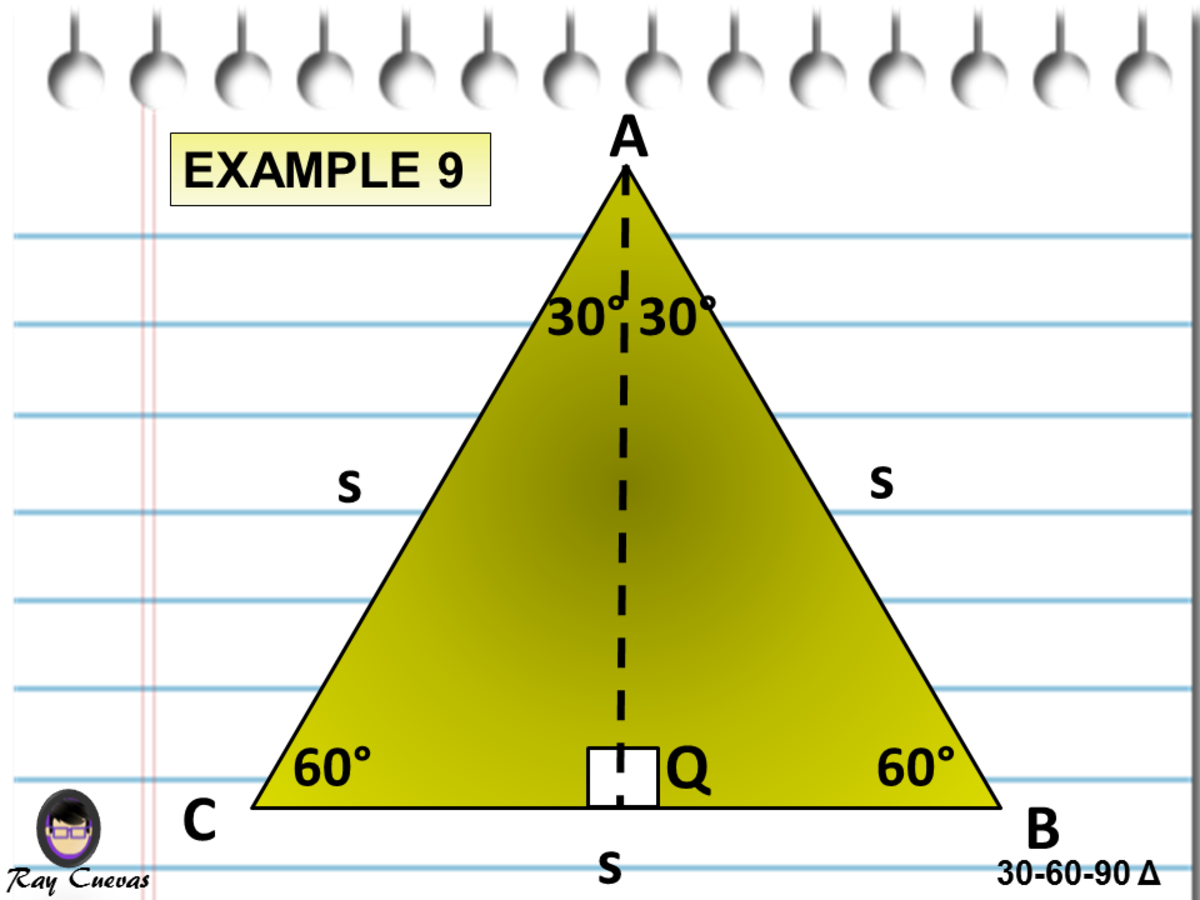
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video




45 45 90 Triangle Theorem Rules Formula Video Lesson Transcript Study Com



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




He Length Of The Hypotenuse Of A 30 60 90 Triangle Is 13 Meters Find The Length Of The Side Brainly Com




30 60 90 Triangle Calculator Formula Rules



The Easy Guide To The 30 60 90 Triangle




Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangles Video Lessons Examples And Solutions




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Theorem Ratio Formula Video
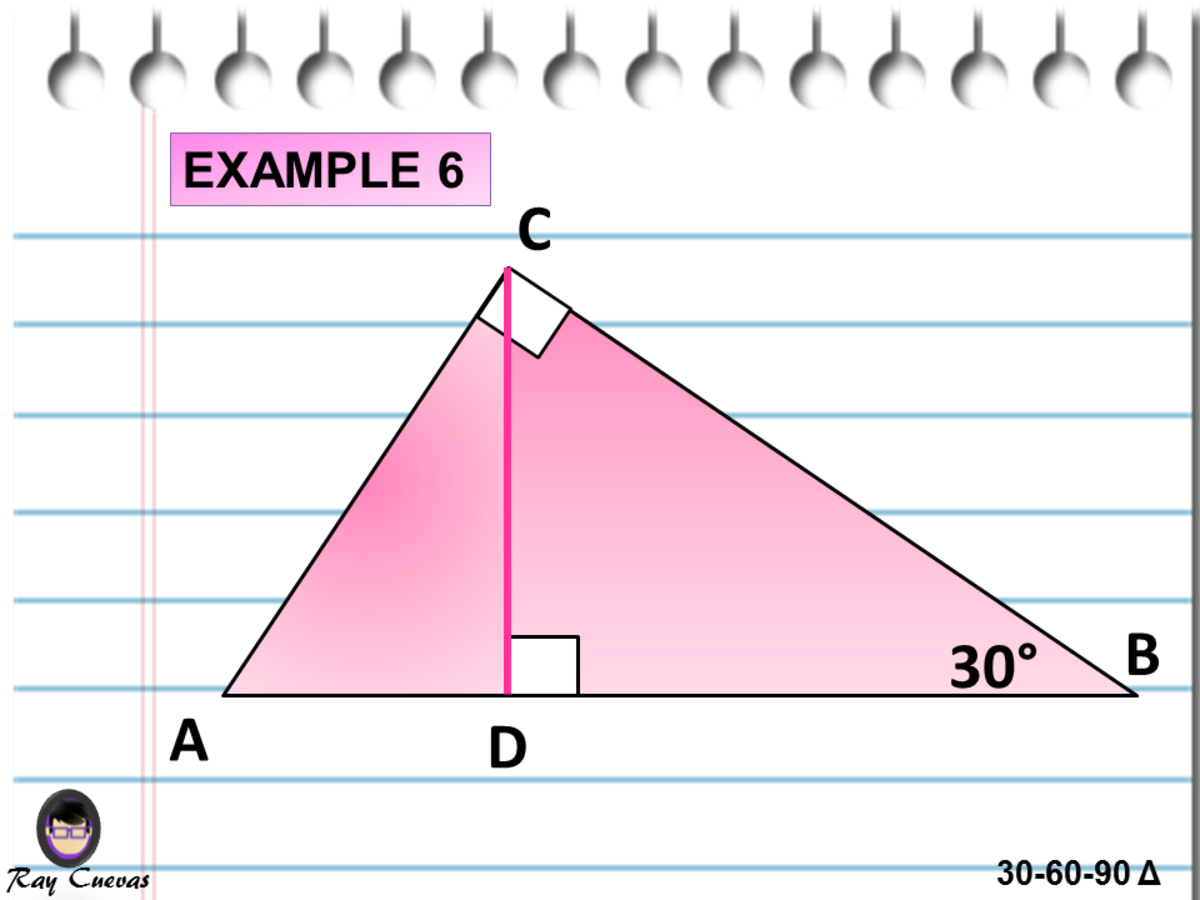



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



The Easy Guide To The 30 60 90 Triangle



1




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



45 45 90 And 30 60 90 Triangles Zona Land Education




A Quick Guide To The 30 60 90 Degree Triangle Dummies



Right Triangles Gmat Free




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



Special Right Triangle 30 60 45 45 37 53 Elearning




30 60 90 Triangle Explanation Examples




30 60 90 Triangles
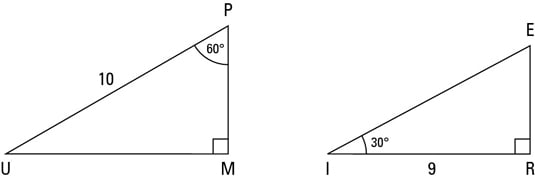



Identifying The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Ratio Formula Video




How To Use The Special Right Triangle 30 60 90 Studypug




A Quick Guide To The 30 60 90 Degree Triangle Dummies



A 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle
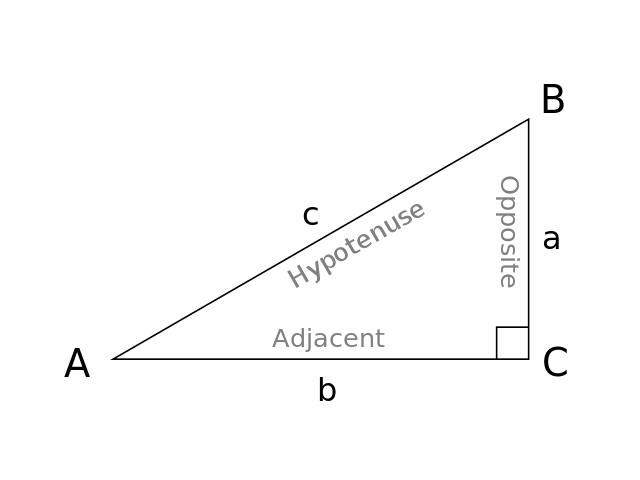



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Theorem Ratio Formula Video



1
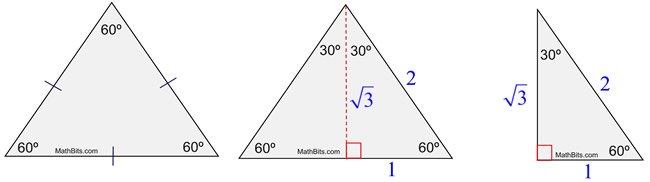



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangles Spock S Guide To Math 4




Act Set 6 Special Right Triangle Rules Flashcards Quizlet




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Proof Don T Memorise Youtube




Chapter 9 Flashcards Quizlet
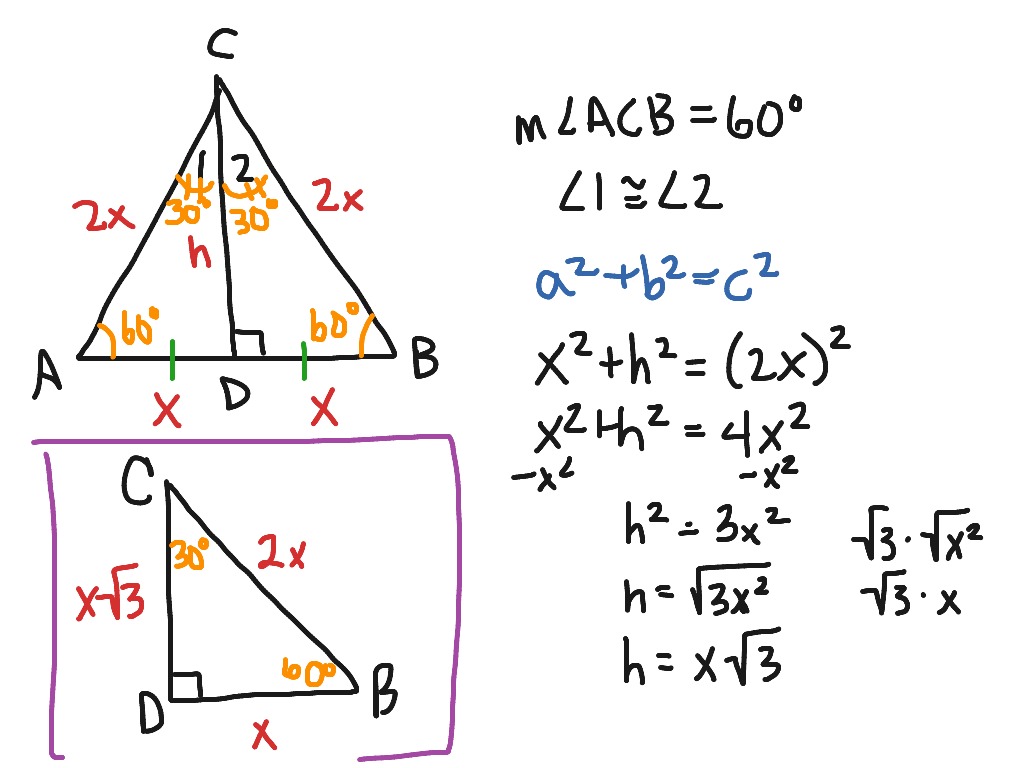



30 60 90 Triangle Math Right Triangles Showme
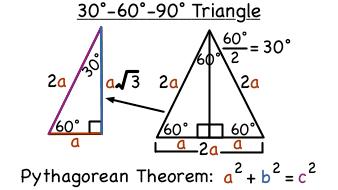



What Is A 30 60 90 Degree Triangle Virtual Nerd Can Help




30 60 90 Triangle Explanation Examples
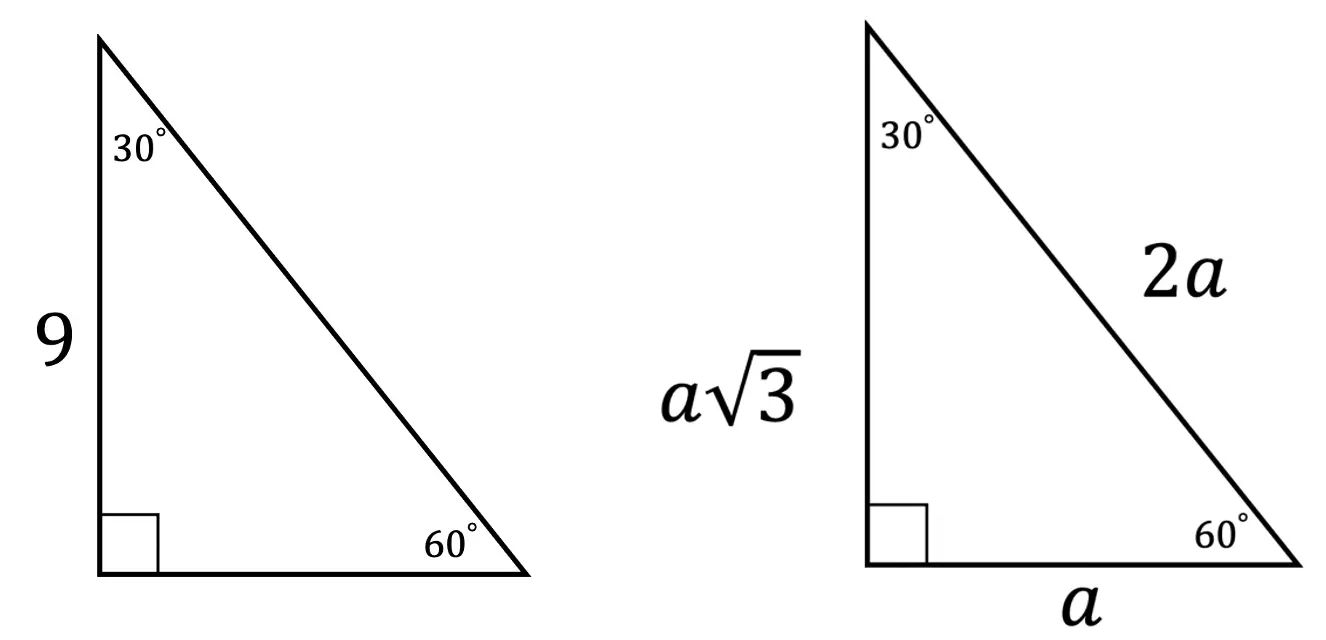



30 60 90 Special Triangles Geometry Mathsux 2




The Complete Guide To The 30 60 90 Triangle



2




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Right Triangles Free Math Help



The Easy Guide To The 30 60 90 Triangle




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies
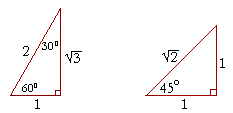



The 30 60 90 Triangle Topics In Trigonometry



How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Right Triangle Side Ratios Expii



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures



Solve A 30 60 90 Triangle With Gradea



1



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangles Hd Youtube




30 60 90 Right Triangles Ck 12 Foundation



30 60 90 Triangle Sides Examples Angles Full Lesson




The 30 60 90 Triangle Topics In Trigonometry



0 件のコメント:
コメントを投稿